※10/16(日): 遊タイムのボーダーを算出しました
パチンコ期待値研究所のヒデです。
今回は、2022年の海物語のメイン機種の一つである「P大海物語4スペシャル」のスペックの解析をしたいと思います。
基本スペック

| 機種・メーカー | P大海物語4スペシャル・SANYO |
|---|---|
| 導入日 | 2020/12/07 |
| 機種タイプ | 確変 |
| 初当たり確率 | 1/319.6 |
| 確変割合 | 52% |
| 確変時大当たり確率 | 1/39.7 |
| ラウンド数 | 10R |
| 賞球数 | 3&2&15&3&4 |
| 通常時時短回数 | 120回(初回は100回) |
| その他 | 遊タイム搭載(時短350回) |
また、出玉の振り分けは以下のようになっています。
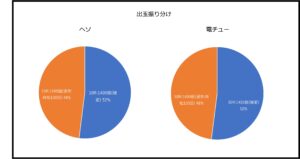
平均継続回数と出玉
ここから独自でシミュレーションを行った結果を載せていきます。
シミュレーション回数は初あたり後の右打ちを100万回試行し、Rというプログラムで結果を算出しています。
平均継続回数(連チャン)
まずは大当たりの連チャンについて見てみましょう。
今回も度数分布表と最大出玉や平均出玉をまとめた表
の2つを用いてまとめています。
| 大当たりの継続回数 | 度数(何%) |
|---|---|
| 1回 | 34.65%(346496回) |
| 2回 | 21.25%(212473回) |
| 3~4回 | 24.08%(240788回) |
| 5~10回 | 18.12%(181196回) |
| 11~20回 | 1.86%(18644回) |
| 21~回 | 0.004%(403回) |
| 指標 | |
|---|---|
| 大当たりの平均継続 | 3.01連 |
| 大当たりのばらつき(標準偏差) | 2.52 |
| 中央値 | 2連 |
| 最大継続回数 | 36連 |
大当たり回数が1回で止まってしまうのが34万回で2回目以降は66万回と
意外にも確変52%でありながら、意外にも1連で終わることは少ないのかと思います。

初当たりの時短100回で大当たりを引ける確率は約27%となっていて
かなり良心的な設定になっていますね。
平均継続回数は3連で中央値は2連と、平均と中央値の値にあまり差がありませんでした。
また、大当たりのばらつき(標準偏差)も2.52とそこまで大きくないので、
この機種が平均的に玉を出す台だと考えられ、個人的にはとても良いなと思います。
平均出玉(獲得玉)
次に獲得玉を見てみましょう。
最初に、出玉の振り分けをグラフにしました。
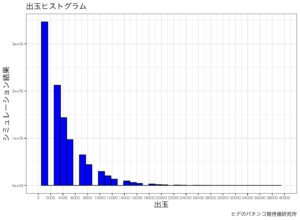
やはり、最初の0~5000発に獲得弾が集中する結果になりました。
次に平均継続回数と同じように、最大出玉といった主要な指標を見てみましょう。
| 指標 | |
|---|---|
| 平均出玉 | 4213.57玉 |
| 最大出玉 | 50400玉 |
| 中央値 | 2800玉 |
平均獲得玉は4213.57玉となりました。
中央値と平均との差は約1400玉とあまり差が見られませんでした。

大海物語は確変か通常かでその差は分かれるものの
当たったら1400発は獲得できるので、平均出玉で見てもそこまでばらつくことはないのかなと思います。
トータル確率・ボーダー
トータル確率は、1/106.19でした。
また、ボーダーと時給の算出は以下のようになりました。
| 換金率|時給 | ボーダー | -1000 | 1000 | 3000 |
|---|---|---|---|---|
| 4円 | 18.96 | 17.32 | 20.95 | 26.50 |
| 3.57円(28球) | 19.70 | 17.93 | 21.85 | 27.97 |
| 3.70円(27球) | 20.50 | 18.59 | 22.84 | 29.60 |
| 3.85円(26球) | 21.25 | 19.20 | 23.77 | 31.18 |
※1:通常時200回転を回した時で時給を計算
遊タイムを考慮したボーダー
遊タイムを考慮したボーダーは以下となりました。
| 残回転数|換金率 | 4円(等価) | 3.03円(33玉) | 3.57円(28玉) | 3.70円(27玉) |
|---|---|---|---|---|
| 残500回転 | 16.68 | 22.00 | 18.68 | 18.02 |
| 残400回転 | 15.81 | 20.87 | 17.71 | 17.09 |
| 残300回転 | 14.61 | 19.29 | 16.39 | 15.79 |
| 残200回転 | 12.92 | 17.06 | 14.48 | 13.97 |
| 残100回転 | 10.52 | 13.89 | 11.79 | 11.37 |
まとめ
今回はP大海物語4スペシャルの解析を行いました。
海で好きな機種の一つですので、皆さんも是非使ってみてください。
(遊タイムを考慮した解析はまだ行えていないので、可能であれば再投稿しようと思います。)




